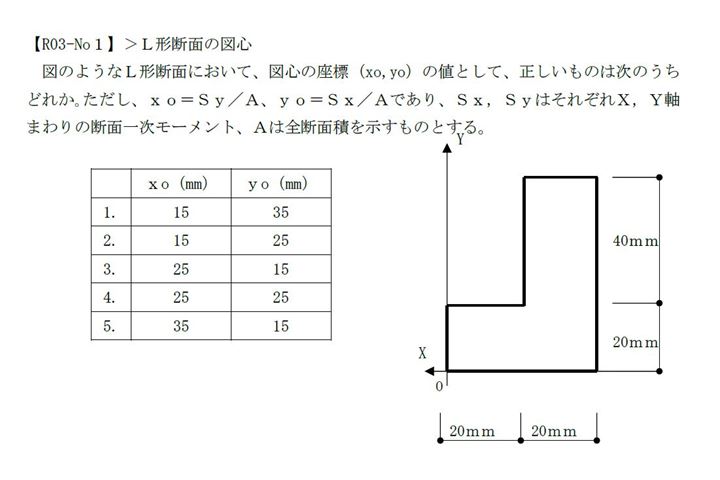
7/4に行われた「2級建築士学科試験」の力学系の問題について、今週の構造系授業で解説を行いました。解法を簡単に説明します。隔年で出題される「図心計算」は断面一次モーメント÷全断面積で求められます。Sx／A＝40000÷1600＝25mm　Sy／A＝40000÷1600＝25mm　となります。同一の問題が平成26年にまったく同じ数値で出題されていますので過去問は非常に大切です。　

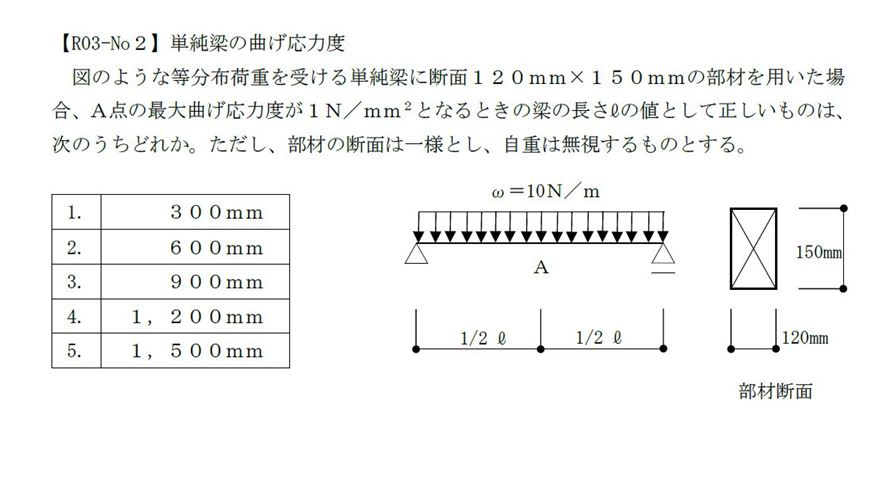
最大曲げ応力MA＝ｗ×Ｌ×Ｌ÷８を断面係数Ｚ＝Ｂ×Ｈ×Ｈ÷６で割った値が曲げ応力度１Ｎ／ｍｍ２であるため

（１０×Ｌ×Ｌ×６）÷（８×１２０×１５０×１５０）＝１　∴Ｌ＝√（１６×１５０×１５０）＝６００ｍｍ　となります。前問同様に平成26年に同じ内容が出題されています。

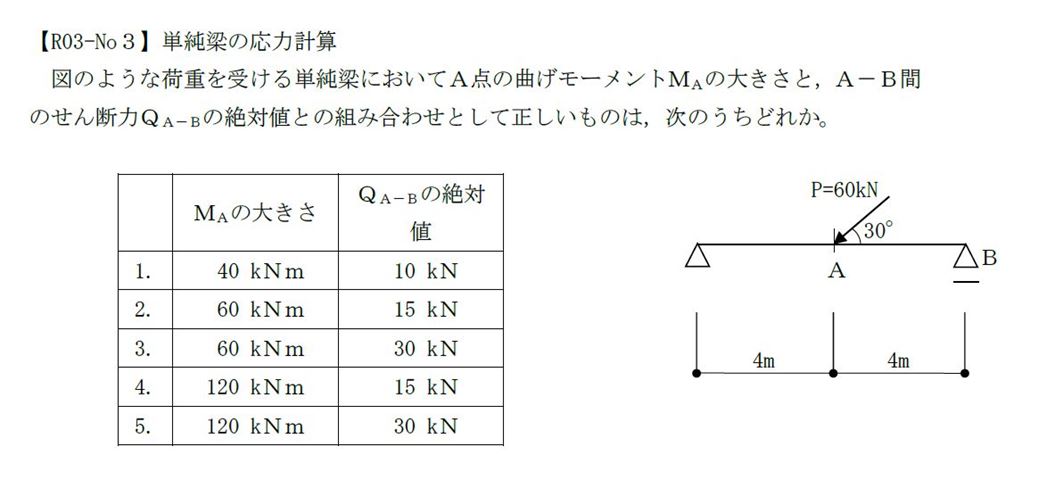
斜めの集中荷重を鉛直方向に分解してPy＝３０kNとし、中央集中荷重で単純梁を解析します反力が集中荷重の半分で１５ｋNとなるので

せん断力Qa-bは１５ｋNです。最大曲げモーメントは反力×４ｍなのでＭＡ＝１５ｋN×４ｍ＝６０ｋＮｍとなり、これも平成29年に同様の出題が確認できます。

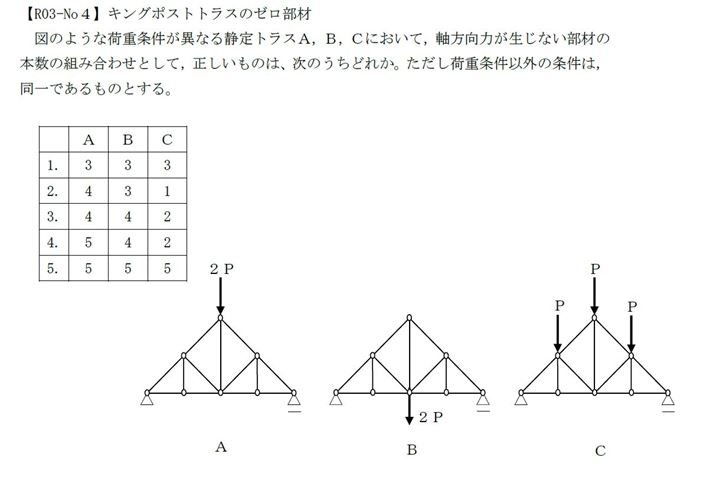
数年に一度出題される、計算不要のトラス問題（サービス問題）です。現役生は教科書「図説やさしい構造力学」P121で解説した軸力ゼロになる条件があてはまります。3部材のうち2部材が一直線になっていると残り部材は必ず軸力ゼロとなります。それを探し出して、A：5部材、B：4部材、C：２部材という答えにたどり着けます。

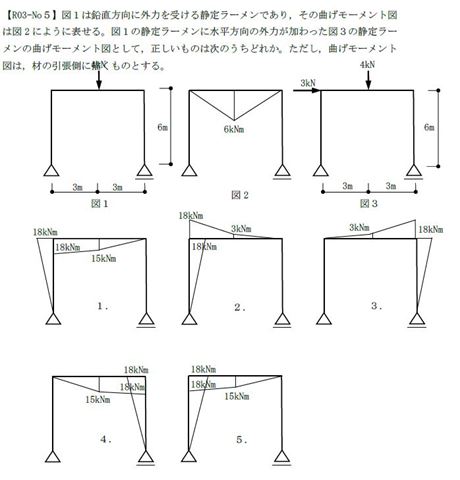
最近数年でラーメンの応力図が頻繁に出題されています。応力数値を計算するのは大変ですが、実はこの場合だと、右下のローラー支点には、水平反力が発生しないため、右側の柱には曲げモーメントは生じません。それと梁柱の端部応力の出る側を考えると、正解は5番しかありません。

弾性座屈荷重の計算公式を言葉に直すと上記のような設問になります。公式はPk＝（π×π×E×I）÷（ℓｋ×ℓｋ）なので、分子が比例関係、分母が反比関係というだけの文章です。ヤング係数は分子にあるので設問の反比例が間違いとなりますので、計算公式を冷静に日本語にすれば大丈夫です。
以上のように、計算の難しさよりも基本項目が身についているかどうかが最大の解答ポイントになりそうです。加えて過去7年以上の過去問が出題されることが散見されますので、昔の問題も機会があれば探ってみましょう。